Core notions

The core notions explained here concern strings, catenae, components, and constituents. A final section addresses formal properties of these terms.

Strings

Catenae

Components

Constituents

Formal properties

A string is defined as a word or a combination of words that is continuous with respect to precedence. Let's break this definition down into its parts. The understanding of the parts of the definition is relevant to the understanding of catenae. We begin from the end of the definition and work our way forward.

Precedence

When two words A and B are immediately next to each other, so that there is no word C appearing between A and B, then A and B are adjacent or contigue. We will say here that either A precedes B, or that B precedes A. Note that precedence is a transitive relationship. If we have an expression such as A B C, then A precedes C by virtue of the fact that A precedes B, and B precedes C.

Continuous

Precedence is continuous if every word of an expression immediately precedes another word of that expression, or is immediately preceded by another word of that expression. In A B C precedence is continuous because A immediately precedes B, and B immediately precedes C. But if we pick just A and C, then A...C is not anymore an instance of continuous precedence because A doesn't immediately precede C. The symbol "..." points to a gap, i.e. non-continuous precedence, between the words immediately to the left and right of the symbol.

Word combination

A combination of words is any set of words that one can create from a given expression. Here, we're concentrating on word combinations built on continuous precedence. Look at the following example:

People like little dogs

Let's try to find combinations of words that obey continuous precedence. We get:

the two-word combinations: People like, like little, little dogs,
the three-word combinations: People like little, like little dogs,
and the four-word combination: People like little dogs.

The word combinations above are all strings because they all obey continuous precedence. Because the words of the word combination People...little, People...dogs, like...dogs, and People...little dogs do not obey continuous precedence, they don't qualify as strings.

There are, however, two problems with concentrating on strings: the first problem is that we may exclude word combinations that are very important for syntactic analysis but which are not strings. The second problem is that over the last half century, linguists have come the conclusion that syntactic structure is not solely based on strings. Rather there is a hidden dimension to language. This dimension is called dominance.

Catena is Latin and means "chain"; its plural is catenae. A catena is defined as a word or a combination of words that is continuous with respect to dominance.

Dominance

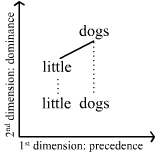
We can understand strings as the "natural" order of words in expressions. This is called linear order. Let's take linear order as the first dimension. In order to understand dominance, let's look at one of the word combinations above, namely little dogs: even though these two words qualify as a string, there is more to say about them. When we talk of little dogs, we talk about dogs. The adjective little is just a qualifier that makes clear that we're not talking about any kind of dogs but about dogs that are little. Or put differently, we're talking about dogs that are little, not about little-ness that is somehow doggish. Because we're talking about dogs regardless of whether we say little dogs or just dogs, we can see that dogs plays are more prominent role than little. Then we say that dogs dominates little, or that little depends on dogs. Dependency, i.e. the idea that some words depend on other words, is the core notion of a class of grammars called dependency grammars.

Dominance is the hidden second dimension. This second dimension is visualized as perpendicular to the first dimension. It looks like this:

The horizontal dimension shows linear order or precedence; here we see on the lower line that little properly precedes dogs. Dominance is shown in the vertical dimension; here we see that little depends on dogs, or conversely that dogs dominates little. The whole picture is called a tree, or more precisely a dependency tree. The angled straight edge is called a dependency edge, and the slightly dotted, vertical edges are called projection edges.
We then see that little dogs isn't only a string, but that dogs also dominates little. But dogs would continue to dominate little even if other words separated them, as in little cute dogs. Look at the next tree:

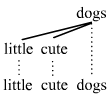
In the tree above, we see that cute separates little and dogs so that they don't form a string anymore. That means that being a string alone would be insufficient to allow the word combination little...dogs, even though these two words clearly have an important relationship.

We can now add to the list of the string word combinations non-string word combinations, namely:

two-word combinations: people...little, people...dogs, like...dogs,
and three-word combinations: people...little dogs, people like...dogs, like little dogs

Not all of these word combinations are important to syntactic analysis, however, and in order to understand which ones are important we need to understand what it means for dominance to be continuous.

Continuous

We have already established that dogs dominates little in little dogs. One of the non-string word combinations, namely like...dogs, also shows dominance: like dominates dogs. The expression like...dogs means "the liking of dogs", rather than the "dogging of likes", because we're talking about liking something, rather than dogs. Similar to little, which qualifies dogs, dogs qualifies like in like...dogs. The difference between little in little dogs, and dogs in like...dogs is that we can omit little, but not dogs. The word little in little dogs is an adjunct of dogs, while the word dogs in like...dogs is an argument of like. Adjuncts can always be omitted, while arguments can only be omitted under certain conditions. In People like little dogs, we cannot omit dogs without the result People like little to be bad.

We now have the situation that like dominates dogs, and dogs dominates little. Does like also dominate little? The answer is yes, but this kind of dominance is not continuous because little doesn't depend on like. Recall that we established that little depended on dogs. That means that while like little is a non-continuous or non-immediate dominance relation it isn't a continuous or immediate dominance relation.

All parts of the definition are now accounted for, and we can proceed to look again at the word combinations.

Catenae: words and combinations of words that are continuous with respect to dominance

Consider first that every single word People, like, little, and dogs is a catena by virtue of the definition. In order to account for the hidden dominance relations, look at the next tree:

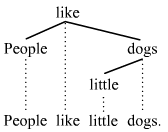
In order to qualify as a catena, a word combination must consist of all words through which one has to trace a continous path from one word to another. Consider People like...dogs, which isn't a string because little is missing. We can trace a continuous path from People through like to dogs, and since the word combination includes all the words one must pass through we're talking about a catena. Consider as a counter example the word combination People like little, which is a string. We start with People, and reach like, but we have no direct path to little. In order to reach little, we would have to pass through dogs, but dogs is not included in the words of the word combination People like little. Therefore People like little is not a catena.

The next table shows all possible word combinations, and gives information on strings and catenae:

Word combinations	String	Catena
People like	+	+
People...little	-	-
People...dogs	-	-
People like little	+	-
People like...dogs	-	+
People like little dogs	+	+
like little	+	-
like...dogs	-	+
like little dogs	+	+
little dogs	+	+

If a word combination has a "+" in the catena column then it is a catena. Those word combinations that have a "+" in the string column and the continuous dominance column qualify as components. The next section will explain this notion.

Components are word combinations that are strings as well as catenae. When we look at the table above again we find that some word combinations are strings, some are catenae, while some are components. Yet some word combinations qualify as nothing at all, and we can conclude that these word combinations aren't important in syntactic analysis. Let's look again at the table with more information:

Some components are again more important than others. People like little dogs and little dogs, for instance differ from People like and like little dogs in that the former are constituents. The next section will explain this notion.

Constituents

Constituents are thought to be of primary importance in syntax. Here, we can define a constituent as any complete component. A component is complete if it includes all dependents. Let's look at the component People like: we know it's a component because it is a string and a catena. But we also know that like has yet another dependent, namely dogs. But dogs is not part of the component People like. Hence, People like isn't complete, and thus it fails to be a constituent.
The same is true for the component like little dogs, which is a string and a catena. But again, People is a dependent of like, but not included in like little dogs. Therefore like little dogs is not a constituent because it isn't complete.
On the other hand, the component little dogs is complete because it includes all dependents. little is the only dependent of dogs, and since little doesn't dominate anything, the word combination little dogs is complete, hence a constituent. The entire sentence People like little dogs is, of course, also complete and thus a constituent.
We can now augment our table with this additional notion, and we can also include the individual words:

The notions strings, catenae, components, and constituents entertain certain formal relationships. Components, for instance, are included into the set of strings and the set of catenae. Constituents again form a subset of components, namely that of complete components. We look first at these subsets.

Sets and subsets

The set of strings and the set of catenae overlap, and that overlap forms the set of components. These sets are non-fuzzy, i.e. a word combination either belongs to a set or it doesn't. Within the set of components there is a subset characterized by completeness: within this subset all components are complete. This subset of components is labeled "constituents". The diagram below visualizes these properties:

Hyperonymy and hyponymy

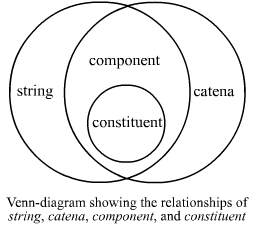
The formal properties of the terms strings, catenae, components, and constituents dictate inheritance. If an expression is a constituent, then it is a component. And if an expression is a component, then it is a string and a catena.
The linguistically salient property of constituents is that they always qualify as catenae. However, not every catena qualifies as a constituent. This is because the notion catena is a hyperonym to constituent. Constituents must always fulfill three criteria:

1. Constituents must be strings.
2. Constituents must be catenae.
3. Constituents must be complete.

Inclusivity and exclusivity

Since constituents must fulfill the above three criteria, it follows that fewer word combinations will qualify as constituents, than will as strings, catenae, or components. A notion A is more inclusive than another notion B, if in a given expression C more word combinations qualify as A than as B. E.g. looking at the last table, we find that 10 expressions qualify as catenae, 8 expressions qualify as components, and 4 expressions qualify as constituents. This corresponds to the formal properties explicated above: catenae are more inclusive than components, which again are more inclusive than constituents.
Conversely, if a notion A is less inclusive than another notion B, then A is more exclusive than B, i.e. A excludes more word combinations in a given expression C than B does. The constituent is a very exclusive notion, as it excludes many word combinations, but includes only few.
The degree of exclusivity of the notion constituent has occluded parsimonious solutions to syntactic problems, because exclusive notions require costly operations.

Back